Camera Fundamentals and Parameters in Photogrammetry
Photogrammetry is the science of using photographs to obtain measurements and models of real-world objects and scenes. Photogrammetric techniques involve using known information to help solve other, previously unknown information. Several critical pieces of known information concern the camera used to capture the photographs, and defining those pieces in mathematical terms known as camera parameters.
Photogrammetry uses the mathematics of light rays to build up knowledge of the geometry of the scene, its objects and the location of the camera when the photographs were taken. When light hits part of the scene, it is reflected toward the camera, passes through the lens, and is picked up by film or an electronic image sensor.
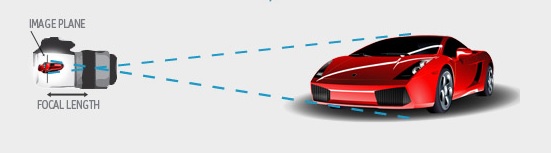
Knowledge of the fundamental parameters of the camera help the photogrammetric software build up the correct geometrical understanding of the relationship of the camera to the scene. Key parameters in a camera that the software needs to know are: focal length, imaging size, sampling characteristics (in the case of digital source images), principal point, and lens distortion. All of this contributes to an understanding of how a light ray, which is picked up by the film or image sensor, was generated by a point in real-world space. The photogrammetry software uses information from multiple light rays to reconstruct the scene in 3D.
Photogrammetry software will either know these internal characteristics beforehand (by completing a calibration procedure), or will figure them out during processing of the scene (referred to as auto-calibration or self/field calibration). Many types of capture devices can provide source images for photogrammetry, including iPhones or other cellphones, point and shoot cameras, DSLRs, surveillance cameras, and more.
Here is a description of each one of these key camera characteristics:
- Focal length. The focal length of a lens determines the magnification and the angle of the light ray. The longer the focal length, the greater the magnification of the image, which is why long telephoto lenses are used to take pictures from far away. A long focal length will also have light rays hit the image sensor at shallower angles. Short focal length lenses cover larger areas in their field of view and are called ‘wide angle’, or ‘fish-eye’ when very wide.
- Imaging size. The size of the film, or the digital sensor’s imaging area determines the geometric relationship between the light ray and a point identified on the photograph. If you keep focal length constant but increase the imaging area size, you will capture more of the scene in the image. The amount of the scene captured in one image is determined by both the focal length and the imaging size. This relationship or ratio (between focal length and image format size) is more important than knowing just one or the other of the parameters. In the days of film cameras the image size was usually 35mm, or sometimes other sizes such as 8mm, 16mm, and 70mm widths. Today’s digital image sensors vary from a couple of millimeters across in a cell phone camera, to 50mm across for very high end sensors.
- Sampling. Modern photogrammetry is carried out in the digital realm by a computer. To this end, we use digital cameras with digital sensors that have pixels covering the imaging area. Each pixel picks up a bit of light from one part of the scene. Photogrammetry software uses the position of where the light ray hits the sensor’s surface to determine the light ray geometry. To get this 2D position from a digital image, one needs the relationship between the pixels in the digital image and the physical sensor size. This is given by the sampling or the pixel size. On some cameras the size of a pixel is only a few microns across – a fraction of the diameter of a human hair!
- Principal point. Photography takes a two-dimensional image of a three-dimensional world. The projection of your three-dimensional scene, through the lens, onto the image plane is a two dimensional representation of the scene. The image plane is the area where the film or the digital image sensor is located. The principal point of an image is the point where a camera’s direct line of sight (called the optical axis) intersects the image plane. This is the image’s mathematical center. For high accuracy photogrammetric work, it is good to know if the lens is mounted centered over the image sensor – due to small manufacturing variances – and hence if the principal point is in the center of the image. This affects the mathematical calculation of the light ray geometry.
- Lens distortion. In an ideal camera (when simulating the lens as one piece), the light ray travels in a straight line from the scene to the imaging surface in the camera. Real lenses are not ideal though and will warp the light ray in interesting ways. This warp varies by the location of the light ray on the image plane. A common form of lens distortion you may have seen is barrel distortion. This distortion causes straight lines in the scene to be curved. Photogrammetry software needs to ‘undo’ lens distortion to build up the correct internal geometry. The lens distortion has to be characterized in a mathematical formula or as a map for accurate results.
[barrel lens distortion]
All of these characteristics or parameters come together to help the photogrammetry software define the important geometric relationships needed to do accurate measurement or modeling. If you need accurate results in photogrammetry, it is good to know your camera parameters accurately. It is also important to determine if these parameters are stable, or else if they change in a material way over time, or in different operating environments such as significant temperature changes. A good camera calibration (whether done before the project processing, or as part of the processing) will help determine these all important camera parameters.
Further information on how photogrammetry works can be found on the PhotoModeler How it Works page.

